مقدمه ای بر توابع هذلولی

مقدمه ای بر توابع هذلولی

عمومی

شش تابع هذلولی شناخته شده عبارتند از : سینوس هذلولی، کسینوس هذلولی ، تانژانت هذلولی ، کوتانژانت هذلولی ، کوسکانت هذلولی و سکانت هذلولی . آنها جزو پرکاربردترین توابع ابتدایی هستند. توابع هذلولی دارای بسیاری از خواص مشترک هستند و خواص و فرمول های زیادی مشابه توابع مثلثاتی دارند.

تعاریف توابع هذلولی

همه توابع هذلولی را می توان به عنوان توابع گویا ساده تابع نمایی تعریف کرد :

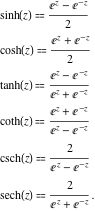توابع , , و همچنین می توانند از طریق توابع و با استفاده از فرمول های زیر تعریف شوند:

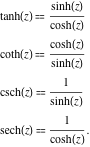نگاهی گذرا به توابع هذلولی

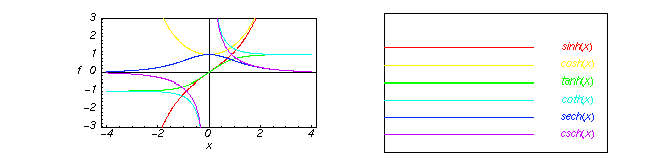
در اینجا نگاهی سریع به گرافیک شش تابع هذلولی در امتداد محور واقعی داریم.

اتصالات درون گروه توابع هذلولی و با سایر گروه های تابعی

بازنمایی از طریق توابع عمومی تر

توابع هذلولی موارد خاصی از توابع عمومی تر هستند. در میان این توابع عمومی‌تر، چهار دسته از توابع ویژه از اهمیت ویژه‌ای برخوردارند: بسل، ژاکوبی، ماتیو و توابع فراهندسی.

به عنوان مثال، و از طریق بسل، ماتیو و توابع فرا هندسی، نمایش های زیر را داشته باشید:

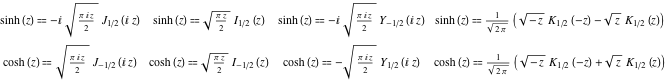همه توابع هذلولی را می توان به عنوان موارد منحط توابع بیضوی متناوب مضاعف Jacobi نشان داد که پارامتر دوم آنها برابر یا برابر باشد :

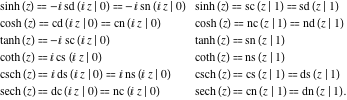بازنمایی از طریق توابع معادل مرتبط

هر یک از شش تابع هذلولی را می توان از طریق تابع مثلثاتی مربوطه نشان داد:

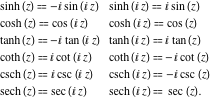روابط با توابع معکوس

هر یک از شش تابع هذلولی با دو فرمول با یک تابع هذلولی معکوس مرتبط است. یک جهت را می توان از طریق یک فرمول ساده بیان کرد، اما جهت دیگر به دلیل ماهیت چند ارزشی تابع معکوس بسیار پیچیده تر است:

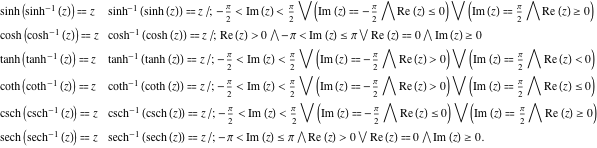بازنمایی از طریق دیگر توابع هذلولی

هر یک از شش تابع هذلولی را می توان از طریق هر تابع دیگری به عنوان تابع منطقی آن تابع با یک آرگومان خطی نشان داد. به عنوان مثال، سینوس هذلولی می تواند به عنوان یک تابع تعریف کننده گروه باشد زیرا پنج تابع دیگر را می توان به صورت زیر بیان کرد:

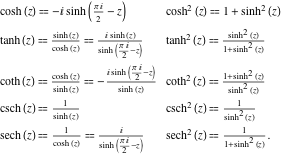هر شش تابع هذلولی را می توان به هر تابع دیگری از گروه توابع هذلولی تبدیل کرد اگر آرگومان با :

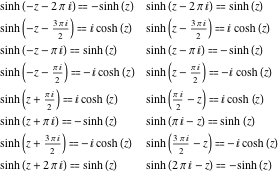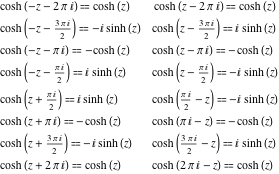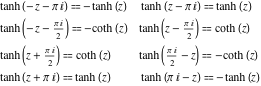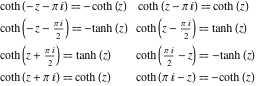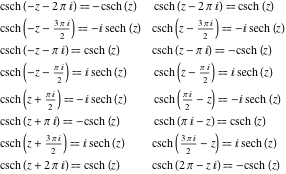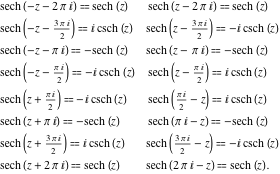شناخته شده ترین خواص و فرمول های توابع هذلولی

مقادیر واقعی برای استدلال های واقعی

برای مقادیر واقعی آرگومان ، مقادیر تمام توابع هذلولی واقعی (یا بی نهایت) هستند.

در نقاط ، مقادیر توابع هذلولی جبری هستند. در چندین مورد، آنها حتی می توانند اعداد گویا باشند، یا (به عنوان مثال ، یا ). اگر و حاصل ضرب توان 2 و اعداد اول متمایز فرما {3، 5، 17، 257، ...} باشد، آنها را می توان تنها با استفاده از ریشه های مربع بیان کرد .

مقادیر ساده در صفر

همه توابع هذلولی مقادیر نسبتاً ساده ای برای آرگومان ها دارند و :

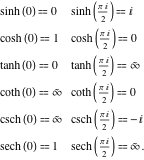تحلیل گرایی

همه توابع هذلولی برای همه مقادیر مختلط تعریف شده اند ، و آنها توابع تحلیلی در کل صفحه مختلط هستند و برش شاخه یا نقاط انشعاب ندارند. این دو تابع و کل توابع با یک نقطه مفرد ضروری در هستند . همه توابع هذلولی دیگر توابع مرومورفیک با قطب های ساده در نقاط (برای و ) و در نقاط (برای و ) هستند.

دوره ای

همه توابع هذلولی توابع تناوبی با دوره واقعی ( یا ) هستند:

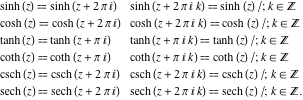برابری و تقارن

همه توابع هذلولی دارای برابری (فرد یا زوج) و تقارن آینه ای هستند:

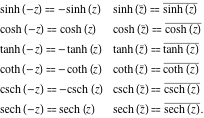نمایش ساده مشتقات

مشتقات همه توابع هذلولی دارای نمایش های ساده ای هستند که می توانند از طریق دیگر توابع هذلولی بیان شوند:

معادلات دیفرانسیل ساده

راه‌حل‌های ساده‌ترین معادله دیفرانسیل معمولی خطی مرتبه دوم با ضرایب ثابت را می‌توان از طریق و نشان داد . سایر توابع هذلولی معادلات دیفرانسیل غیرخطی مرتبه اول را برآورده می کنند:

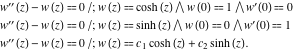هر شش تابع هذلولی معادلات دیفرانسیل غیرخطی مرتبه اول را برآورده می کنند:

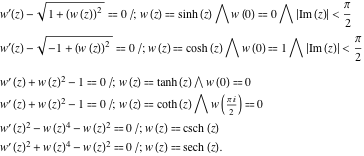کاربرد توابع هذلولی

توابع مثلثاتی ارتباط نزدیکی با هندسه مثلث دارند. توابعی مانند سینوس و کسینوس اغلب به عنوان طول لبه های مثلث قائم الزاویه معرفی می شوند. توابع هذلولی در نظریه مثلث ها در فضاهای هذلولی رخ می دهند.

لوباچفسکی (1829) و جی. بولای (1832) به طور مستقل این فرضیه پنجم اقلیدس را تشخیص دادند - که می‌گویند برای یک خط معین و نقطه‌ای که روی خط نیست، دقیقاً یک خط موازی با خط اول وجود دارد - ممکن است تغییر کند و همچنان یک خط ثابت باشد. هندسه. در هندسه هذلولی، مجاز است بیش از یک خط موازی با خط اول باشد (به این معنی که خطوط موازی هرگز به خط اول نمی رسند، هر چقدر هم که امتداد داشته باشند). ترجمه شده به مثلث، به این معنی است که مجموع سه زاویه همیشه کمتر از .

یک نمایش خاص از هندسه هذلولی را می توان در دیسک واحد اعداد مختلط (مدل دیسک پوانکاره) تحقق بخشید. در این مدل، نقاط اعداد مختلط در دیسک واحد هستند و خطوط یا کمان‌هایی از دایره‌هایی هستند که مرز دایره واحد را متعامد یا قطرهای دایره واحد را برآورده می‌کنند.

فاصله بین دو نقطه (به معنی اعداد مختلط) و در دیسک پوانکاره برابر است با:

ویژگی جذاب مدل دیسک پوانکاره این است که زوایای هذلولی با زوایای اقلیدسی مطابقت دارند. به طور رسمی، زاویه در یک نقطه از دو خط هذلولی و با فرمول توصیف می شود:

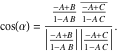در ادامه، مقادیر سه زاویه یک مثلث هذلولی در رأس , و با , و نشان داده می شود . طول هذلولی سه یال مقابل زوایا نشان داده می شود ، و .

قانون کسینوس و قانون کسینوس دوم برای مثلث های هذلولی عبارتند از:

قانون سینوس برای مثلث های هذلولی به این صورت است:

برای یک مثلث قائم الزاویه، نسخه هذلولی قضیه فیثاغورث از فرمول های قبلی پیروی می کند (زاویه قائمه در راس گرفته می شود ):

با استفاده از بسط سری در مقیاس های کوچک، هندسه هذلولی با هندسه اقلیدسی آشنا تقریب زده می شود. فرمول کسینوس و فرمول سینوس برای مثلث های هذلولی با زاویه قائمه در راس تبدیل می شوند:

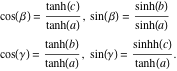دایره محاط شده دارای شعاع است:

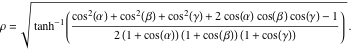دایره محصور دارای شعاع زیر است:

برنامه های کاربردی دیگر

به عنوان توابع منطقی تابع نمایی، توابع هذلولی تقریباً در همه جا در علوم کمی ظاهر می شوند. فهرست کردن کاربردهای متعدد آنها در تدریس، علم، مهندسی و هنر غیرممکن است.