شعاع همگرایی

ساخت وبلاگ

آخرین مطالب

امکانات وب

شعاع همگرایی


از ویکیپدیا، دانشنامه آزاد

پرش به ناوبریپرش به جستجو

در ریاضیات ، شعاع همگرایی یک سری قدرت ، شعاع بزرگترین دیسکی است که مجموعه در آن جمع می شود . یا یک عدد واقعی غیر منفی است یا بی فایده . هنگامی که آن را مثبت است، این سری قدرت مطلقا همگرا و یکنواخت در مجموعه های جمع و جور در داخل دیسک باز شعاع به شعاع همگرایی برابر، و آن است سری تیلور از تابع تحلیلی است که به آن همگرا.

فهرست

برای یک سری قدرت ƒ تعریف می شود:

f (z) = sum_ {n = 0} ^ کمبود c_n (za) ^ n ،

جایی که،

a یک ثابت پیچیده است ، مرکز دیسک همگرایی ،

ج نفر است N هفتم ضریب پیچیده، و

z یک متغیر پیچیده است.

شعاع همگرایی r یک عدد واقعی غیر منفی است یا بی فایده  به گونه ای که سری اگر

| za | <r ،

و اگر واگرایی کند

| za | > r. ،

برخی ممکن است یک تعریف جایگزین را ترجیح دهند ، زیرا وجود واضح است:

{ displaystyle r = sup left {| za | left | sum _ {n = 0} ^ { infty} c_ {n} (za) ^ {n} { text {converges} } راست. راست }}

در مرز ، یعنی جایی که | z  -  a | = r ، رفتار سری قدرت ممکن است پیچیده باشد و این سری ممکن است برای برخی از مقادیر z جمع شده و برای برخی دیگر واگرایی کند. شعاع همگرایی نامحدود است اگر مجموعه برای همه اعداد مختلط z جمع شود . [1]

یافتن شعاع همگرایی [ ویرایش ]

دو مورد پیش می آید. حالت اول نظری است: وقتی همه ضرایب را بدانیدc_ {n}سپس محدودیت های خاصی را در نظر می گیرید و شعاع دقیق همگرایی را پیدا می کنید. حالت دوم عملی است: هنگامی که شما یک حل مشکل مشکل را با استفاده از سری سری ایجاد می کنید ، معمولاً فقط یک تعداد محدود اصطلاحات را در یک سری قدرت می دانید ، از چند اصطلاح تا صد اصطلاح. در این حالت دوم ، برون یابی طرح ، شعاع همگرایی را تخمین می زند.

شعاع نظری [ ویرایش ]

شعاع همگرایی را می توان با استفاده از آزمون ریشه در اصطلاحات سری پیدا کرد. تست ریشه از عدد استفاده می کند

{ displaystyle C = limsup _ {n rightarrow infty} { sqrt [{n}] {| c_ {n} (za) ^ {n} |}} = limsup _ {n rightarrow infty} چپ ({ sqrt [{n}] {| c_ {n} |}} راست) | za |}

"lim sup" نشان دهنده حد برتر است . آزمایش ریشه بیان می کند که این سری در صورت C  <1 همگرایی می کند و در صورت  C  > 1 از هم جدا می شود. از این رو اگر فاصله فاصله از z تا مرکز a کمتر از این باشد ، سری قدرت همگرا می شود.

r = frac {1} { limsup_ {n rightarrow infty} sqrt [n] {| c_n |}}

و اگر فاصله از آن عدد بیشتر شود ، اختلاف می یابد. این عبارت قضیه کوشی - هادامارد است . توجه داشته باشید که r  = 1/0 به عنوان شعاع بی نهایت تفسیر می شود ، به این معنی که ƒ یک تابع کامل است .

حد درگیر در آزمون نسبت معمولاً آسانتر محاسبه می شود و وقتی این حد وجود داشته باشد ، نشان می دهد که شعاع همگرایی محدود است.

{ displaystyle r = lim _ {n rightarrow infty} left | { frac {c_ {n}} {c_ {n + 1}}} right |.}

این به شرح زیر نشان داده شده است. آزمون نسبت می گوید اگر سری جمع شود

lim_ {n to infty} frac {| c_ {n + 1} (za) ^ {n + 1} |} {| c_n (za) ^ n |} <1

که برابر است با

| z - a | < frac {1} { lim_ {n to infty} frac {| c_ {n + 1} |} {| c_n |}} = lim_ {n to infty} left | frac { c_n} {c_ {n + 1}} راست |.

برآورد عملی شعاع در مورد ضرایب واقعی [ ویرایش ]

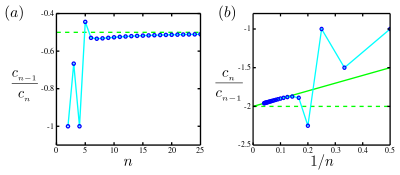
نمودارهای عملکرد f ( varepsilon) = frac { varepsilon (1+ varepsilon ^ 3)} { sqrt {1 + 2 varepsilon}}.
خط سبز جامد یک مجانب خط مستقیم در نمودار Domb – Sykes [2] ، نمودار (b) است که محور عمودی را در −2 قطع می کند و دارای شیب 1+ است. بنابراین یک تکینگی در وجود دارد{ displaystyle varepsilon = -1 / 2} و بنابراین شعاع همگرایی است { displaystyle r = 1/2.}

معمولاً در کاربردهای علمی فقط تعداد محدودی از ضرایب وجود دارد c_ {n}شناخته شده اند به طور معمول ، [ مبهم ] به عنوانnافزایش می یابد ، این ضرایب به یک رفتار منظم تبدیل می شوند که با نزدیکترین تکین محدود کننده شعاع تعیین می شود. در این مورد ، دو تکنیک اصلی ساخته شده است ، بر این اساس که ضرایب یک سری تیلور تقریباً نمایی با نسبت هستند1 / r جایی که r شعاع همگرایی است.

{ displaystyle b_ {n} ^ {2} = { frac {c_ {n + 1} c_ {n-1} -c_ {n} ^ {2}} {c_ {n} c_ {n-2} - c_ {n-1} ^ {2}}} quad n = 3،4،5 ، ldot.}

بسیاری از موارد شناخته شده را ترسیم کنید b_ {n} در مقابل 1 / n، و به صورت گرافیکی برون یابی به 1 / n = 0از طریق تناسب خطی. رهگیری با1 / n = 0 متقابل شعاع همگرایی را تخمین می زند ، 1 / r.

این روش همچنین دو ویژگی دیگر از همگرایی را محدود می کند که تکینگی را محدود می کند. فرض کنید نزدیکترین تکینگی درجه باشدپ و دارای زاویه است { displaystyle pm theta}به محور واقعی سپس شیب تناسب خطی داده شده در بالا می باشد{ displaystyle - (p + 1) / r}. علاوه بر این ، طرح{ displaystyle { frac {1} {2}} سمت چپ ({ frac {c_ {n-1} b_ {n}} {c_ {n}}} + { frac {c_ {n + 1}} {c_ {n} b_ {n}}} راست)} در مقابل 1 / n ^ {2}، و سپس یک برازش مناسب به صورت { displaystyle 1 / n ^ {2} = 0} رهگیری در  cos theta .

شعاع همگرایی در تحلیل پیچیده [ ویرایش ]

با در نظر گرفتن یک متغیر پیچیده ، یک سری توان با شعاع مثبت همگرایی را می توان به یک تابع هولوومرفیک تبدیل کرد . شعاع همگرایی را می توان با قضیه زیر مشخص کرد:

شعاع همگرایی یک سری سری ƒ متمرکز بر یک نقطه a برابر است با فاصله از a تا نزدیکترین نقطه که نمی توان ƒ را به گونه ای تعریف کرد که آن را هولومورفیک کند.

مجموعه کلیه نقاطی که فاصله آنها با a کاملاً کمتر از شعاع همگرایی باشد دیسک همگرایی نامیده می شود .

نمودار توابع توضیح داده شده در متن: تقریب ها با رنگ آبی ، دایره همگرایی با رنگ سفید

نزدیکترین نقطه یعنی نزدیکترین نقطه در صفحه پیچیده ، لزوماً روی خط واقعی نیست ، حتی اگر مرکز و همه ضرایب واقعی باشند. به عنوان مثال ، عملکرد

{ displaystyle f (z) = { frac {1} {1 + z ^ {2}}}}

از آنجا که هیچ یک از ویژگی های خاص در خط واقعی است 1 + z ^ 2هیچ ریشه واقعی ندارد. سری تیلور آن در حدود 0 توسط

sum_ {n = 0} ^ بی اعتبار (-1) ^ nz ^ {2n}.

آزمون ریشه نشان می دهد که شعاع همگرایی آن 1 است. مطابق با این ، تابع ƒ ( z ) در ± i دارای یکتایی است که در فاصله 1 از 0 است.

برای اثبات این قضیه ، به تجزیه و تحلیل توابع هولومورفیک مراجعه کنید .

یک مثال ساده [ ویرایش ]

عملکرد محاوره ای مثلثات را می توان در یک سری توان گسترش داد:

{ displaystyle arctan (z) = z - { frac {z ^ {3}} {3}} + { frac {z ^ {5}} {5}} - { frac {z ^ {7} } {7}} + cdots.}

به راحتی می توانید آزمایش ریشه را در این حالت انجام دهید تا دریابید که شعاع همگرایی 1 است.

مثال پیچیده تر [ ویرایش ]

این سری قدرت را در نظر بگیرید:

{ displaystyle { frac {z} {e ^ {z} -1}} = sum _ {n = 0} ^ { infty} { frac {B_ {n}} {n!}} z ^ { n}}

که در آن اعداد گویا B N هستند اعداد برنولی . ممکن است تلاش برای استفاده از آزمون نسبت برای یافتن شعاع همگرایی این سری کار دشواری باشد. اما قضیه تحلیل پیچیده ای که در بالا بیان شد به سرعت مسئله را حل می کند. در z = 0 ، از آنجا که تکینگی قابل جدا شدن است ، هیچ تکینگی وجود ندارد . بنابراین تنها تکینگی های غیرقابل حذف در نقاط دیگر واقع می شوند که مخرج صفر است. ما حل می کنیم

e ^ z-1 = 0 ،

با یادآوری اینکه اگر z = x  +  iy و e iy  = cos ( y ) +  i  sin ( y ) سپس  

e ^ z = e ^ xe ^ {iy} = e ^ x ( cos (y) + i sin (y)) ، ،

و سپس x و y را واقعی بگیرید. از آنجا که y واقعی است ، مقدار مطلق cos ( y ) +  i  sin ( y ) لزوماً 1 است. بنابراین ، مقدار مطلق e z می تواند 1 باشد فقط اگر e x 1 باشد. از آنجا که x واقعی است ، این فقط در صورت x = 0 اتفاق می افتد بنابراین z خالص خیالی است و cos ( y ) +  i  sin ( y ) = 1. از آنجا که y واقعی است ، این فقط در صورت cos ( y ) = 1 و sin ( y ) = 0 ، بنابراین y  یک عدد صحیح از 2 π است . در نتیجه نقاط منفرد این تابع در رخ می دهد

z = یک عدد صحیح صفر غیر صفر از 2 π i .

تکینگی های نزدیک به 0 ، که مرکز گسترش سری قدرت است ، در π 2 π i است . فاصله از مرکز تا هر یک از این نقاط 2 π است ، بنابراین شعاع همگرایی 2 π است .

همگرایی در مرز [ ویرایش ]

اگر سری توان در اطراف نقطه a گسترش یافته و شعاع همگرایی r باشد ، مجموعه تمام نقاط z به گونه ای است که | z - a | = R است دایره به نام مرز از دیسک همگرایی. یک سری قدرت ممکن است در هر نقطه از مرز انحراف داشته باشد ، یا در بعضی نقاط واگرا شود و در نقاط دیگر همگرا شود ، یا در تمام نقاط مرز همگرا شود. بعلاوه ، حتی اگر سریال در هر جایی از مرز (حتی به طور یکنواخت) همگرا شود ، لزوماً کاملاً همگرا نمی شود.

مثال 1: سری توان برای تابع ƒ ( z ) = 1 / (1 - z ) ، در حدود z = 0 گسترش می یابد ، که به سادگی

sum_ {n = 0} ^ کمبود z ^ n ،

شعاع همگرایی 1 دارد و در هر نقطه از مرز واگرا می شود.

مثال 2: سری توان g ( z ) = −ln (1 - z ) ، در حدود z = 0 گسترش یافته است ، که

sum_ {n = 1} ^ بی اعتبار frac {1} {n} z ^ n ،

شعاع همگرایی 1 دارد ، و برای z = 1 واگرایی می کند اما برای تمام نقاط دیگر مرز همگرا است. تابع ƒ ( Z ) در مثال 1 است مشتق از گرم ( Z ) .

مثال 3: سری قدرت

{ displaystyle sum _ {n = 1} ^ { infty} { frac {1} {n ^ {2}}} z ^ {n}}

شعاع همگرایی 1 دارد و کاملاً در هر جایی از مرز همگرایی می کند. اگرh تابع ارائه شده توسط این مجموعه بر روی دیسک واحد، پس یک مشتق از است( h ( Z  برابر استg ( Z ) / Z باG از مثال 2. به نظر می رسد که ساعت ( Z ) است dilogarithm تابع.

مثال 4: سری توانی

{ displaystyle sum _ {i = 1} ^ { infty} a_ {i} z ^ {i} { text {where}} a_ {i} = { frac {(-1) ^ {n-1 }} {2 ^ {n} n}} { text {for}} n = lfloor log _ {2} (i) rfloor +1 { text {، عدد صحیح منحصر به فرد با}} 2 ^ {n -1} leq i <2 ^ {n} ،}

شعاع همگرایی 1 دارد و به طور یکنواخت در کل مرز | z | = 1 ، اما کاملاً در مرز همگرا نیست . [4]

میزان همگرایی [ ویرایش ]

اگر عملکرد را گسترش دهیم

f (x) = sin x = sum ^ { infin} _ {n = 0} frac {(- 1) ^ n} {(2n + 1)!} x ^ {2n + 1} = x - frac {x ^ 3} {3!} + frac {x ^ 5} {5!} - cdots text {برای همه} x

در اطراف نقطه x = 0 ، متوجه می شویم که شعاع همگرایی این سری برابر است scriptstyle ناکارآمدبه این معنی که این مجموعه برای همه اعداد مختلط جمع می شود. با این حال ، در برنامه ها ، اغلب به دقت یک جواب عددی علاقه مند می شود . هم تعداد اصطلاحات و هم مقداری که قرار است سری ارزیابی شود ، در درستی جواب تأثیر دارد. به عنوان مثال ، اگر بخواهیم f (0.1) = sin (0.1) را دقیقاً تا پنج رقم اعشار محاسبه کنیم ، فقط به دو اصطلاح اول سری احتیاج داریم. با این حال ، اگر دقت یکسانی را برای x = 1 می خواهیم ، باید پنج اصطلاح اول سری را ارزیابی و جمع کنیم. برای f (10) ، یکی 18 اصطلاح اول سری را می طلبد ، و برای f (100) 141 اصطلاح اول را باید ارزیابی کنیم.

بنابراین برای این مقادیر خاص ، سریعترین همگرایی انبساط سری قدرت در مرکز است و هرچه فرد از مرکز همگرایی دور می شود ، سرعت همگرایی کاهش می یابد تا زمانی که به مرز برسید (در صورت وجود) و از آن عبور کنید ، در این صورت سریال متفاوت خواهد شد.

Abscissa همگرایی یک سری Dirichlet [ ویرایش ]

یک مفهوم مشابه ، خلاصه همگرایی یک سری دیریشله است

sum_ {n = 1} ^ بی اعتبار {a_n over n ^ s}

چنین همگرا سری اگر بخشی واقعی از بازدید کنندگان بیشتر از یک شماره خاص بسته به ضرایب است N : در بعد افقی همگرایی.

منبع

https://en.wikipedia.org/wiki/Radius_of_convergence 

ریاضیات...
ما را در سایت ریاضیات دنبال می کنید

برچسب : نویسنده : 9math1342d بازدید : 233 تاريخ : جمعه 19 دی 1399 ساعت: 6:16

آرشیو مطالب

پيوندهای روزانه

لینک دوستان

خبرنامه