راه حل های خاص و همگن معادلات پواسون و لاپلاس

فرض کنید می خواهیم یک موقعیت الکتروکوازیستاتیک را همانطور که در شکل 5.1.1 نشان داده شده است، تحلیل کنیم. یک توزیع بار ( r ) در قسمت فضای مورد نظر که با حجم V مشخص شده است مشخص می شود . این منطقه توسط هادی های کامل با شکل و مکان مشخص محدود شده است. پتانسیل های شناخته شده برای این هادی ها و سطح محصور اعمال می شود که ممکن است در بی نهایت باشد.

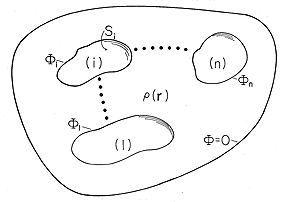
شکل 5.1.1 حجم مورد نظر که می تواند در آن توزیع چگالی بار وجود داشته باشد. برای نشان دادن سطوح مرزی که پتانسیل روی آنها محدود شده است، n سطح جدا شده و یک سطح محصور نشان داده شده است.

در فضای بین هادی ها تابع پتانسیل از معادله پواسون پیروی می کند (5.0.2). راه حل خاصی از این معادله در حجم تجویز شده V توسط انتگرال برهم نهی داده شده است (4.5.3).

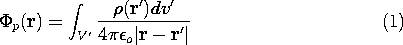
این پتانسیل در هر نقطه از حجم V از معادله پواسون تبعیت می کند . از آنجایی که ما این معادله را خارج از حجم V ارزیابی نمی‌کنیم ، ادغام بر روی منابعی که در (1) فراخوانی شده‌اند، نیازی به هیچ منبع دیگری به جز منابع داخل حجم V ندارند . این امر روشن می کند که راه حل خاص منحصر به فرد نیست، زیرا افزودن به پتانسیل حاصل از ادغام بیش از بارهای دلخواه خارج از حجم V ، تنها باعث ایجاد پتانسیلی می شود که مشتق لاپلاسی آن در حجم V صفر است .

آیا (1) راه حل کامل است؟ از آنجا که منحصر به فرد نیست، پاسخ باید باشد، مطمئناً نه. علاوه بر این، واضح است که هیچ اطلاعاتی در مورد موقعیت و شکل هادی ها در این راه حل وجود ندارد. از این رو، میدان الکتریکی به دست آمده به عنوان گرادیان منفی پتانسیل 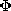p از (1)، به طور کلی، دارای یک جزء مماسی محدود بر روی سطوح الکترودها خواهد بود. از سوی دیگر، هادی ها دارای توزیع بار سطحی هستند که خود را طوری تنظیم می کنند که باعث می شود میدان الکتریکی خالص روی سطوح هادی ها دارای اجزای میدان الکتریکی مماس ناپدید شونده باشد. توزیع این بارهای سطحی در ابتدا مشخص نیست و از این رو نمی توان آن را در انتگرال (1) گنجاند.

راه برون رفت از این معضل به شرح زیر است: توزیع پتانسیلی که ما در فضایی که هادی ها اشغال نمی کنند، نتیجه دو توزیع بار است. اول توزیع بار حجمی تجویز شده است که منجر به تابع پتانسیل 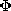p می شود ، و دوم، بار توزیع شده روی سطوح هادی است. تابع پتانسیل تولید شده توسط بارهای سطحی باید از معادله پواسون بدون منبع در فضای V مورد نظر تبعیت کند. اجازه دهید این راه حل را به شکل همگن معادله پواسون با تابع پتانسیل 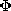h نشان دهیم . سپس در حجم V، 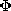h باید معادله لاپلاس را برآورده کند.

سپس اصل برهم نهی نوشتن پتانسیل کل را به عنوان امکان پذیر می کند

مشکل یافتن توزیع کامل میدان اکنون به یافتن راه حلی کاهش می یابد که پتانسیل خالص 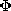(3) دارای پتانسیل های تجویز شده v i در سطوح S i باشد . اکنون 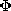p شناخته شده است و می توان آن را در سطح S i ارزیابی کرد . ارزیابی (3) در S i می دهد

به طوری که محلول همگن بر روی مرزهای S i تجویز می شود .

از این رو، تعیین یک میدان الکتروکوازیستاتیک با پتانسیل های تعیین شده بر روی مرزها به یافتن جواب معادله لاپلاس، (2) کاهش می یابد، که شرط مرزی ارائه شده توسط (5) را برآورده می کند.

رویکردی که در این بخش رسمیت یافته است، دیدگاه دیگری است که برای مسائل ارزش مرزی در قسمت آخر فصل قابل استفاده است. 4. مطمئناً، نمای انتزاعی وضعیت ارزش مرزی ارائه شده در شکل 5.1.1 با شکل 4.6.1 تفاوتی ندارد. در مثال 4.6.4، میدان نشان داده شده در شکل 4.6.8 برای بار نقطه ای مجاور یک الکترود کروی با بار خنثی برابر تعیین می شود. در حجم V مورد علاقه در خارج از الکترود، توزیع بار حجمی منفرد است، بار نقطه ای q . پتانسیل داده شده توسط (4.6.35)، در واقع به شکل (3) است. راه حل خاص را می توان به عنوان اولین جمله، پتانسیل شارژ نقطه ای در نظر گرفت. عبارت دوم و سوم که معادل پتانسیل های ناشی از بارهای ساختگی درون کره هستند را می توان به عنوان راه حل همگن در نظر گرفت.

برهم نهی برای ارضای شرایط مرزی

در بخش های بعدی، برهم نهی اغلب به روش دیگری برای برآوردن شرایط مرزی استفاده می شود. فرض کنید که در حجم V چگالی بار وجود ندارد و دوباره پتانسیل های هر یک از n سطح S j v j است . سپس

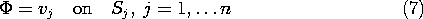
محلول به یک برهم نهی از محلول‌های 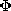j تقسیم می‌شود که شرایط مورد نیاز را در سطح j- امین دارند ، اما در تمام موارد دیگر صفر هستند.

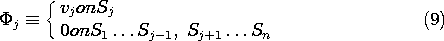
هر جمله راه حلی برای معادله لاپلاس (6) است، بنابراین مجموع آن نیز است.

در ثانیه 5.5، روشی برای برآوردن شرایط مرزی دلخواه در یکی از چهار سطحی که حجم مورد علاقه را در بر می گیرد، توسعه داده شده است.

ماتریس ظرفیت

فرض کنید که در سیستم الکترود n بار خالص روی الکترود i قرار است پیدا شود. با توجه به (8)، انتگرال E d a بر روی سطح S i که این الکترود را در بر می گیرد، سپس

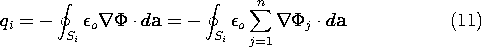
به دلیل خطی بودن معادله لاپلاس، پتانسیل 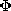j متناسب با ولتاژ تحریک کننده آن پتانسیل، v j است . نتیجه می شود که (11) را می توان بر حسب پارامترهای خازنی که مستقل از تحریکات هستند نوشت. یعنی (11) می شود

جایی که ضرایب خازن هستند

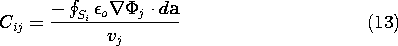
بار روی الکترود i- امین برهم نهی خطی مشارکت همه n ولتاژ است. ضریب ضرب ولتاژ خود، C ii ، خود خازن نامیده می شود ، در حالی که بقیه، C ij ، i j ، ظرفیت های متقابل هستند .