معادله هلمهولتز

ساخت وبلاگ

آخرین مطالب

امکانات وب

معادله هلمهولتز

از ویکیپدیا، دانشنامه آزاد

در ریاضیات، معادله هلمهولتز مسئله مقدار ویژه برای عملگر لاپلاس است . با معادله دیفرانسیل جزئی خطی مطابقت دارد

{displaystyle nabla ^{2}f=-k^{2}f,}که در آن ∇ 2 عملگر لاپلاس، k 2 مقدار ویژه، و f تابع (ویژه) است. هنگامی که معادله برای امواج اعمال می شود، k به عنوان عدد موج شناخته می شود . معادله هلمهولتز کاربردهای مختلفی در فیزیک و علوم دیگر دارد، از جمله معادله موج ، معادله انتشار و معادله شرودینگر برای یک ذره آزاد.

این معادله به نام هرمان فون هلمهولتز ، که آن را در سال 1860 مطالعه کرد، نامگذاری شده است.

انگیزه و موارد استفاده [ ویرایش ]

معادله هلمهولتز اغلب در مطالعه مسائل فیزیکی مربوط به معادلات دیفرانسیل جزئی (PDEs) در فضا و زمان به وجود می آید. معادله هلمهولتز، که شکل مستقل از زمان معادله موج را نشان می‌دهد ، از بکارگیری تکنیک جداسازی متغیرها برای کاهش پیچیدگی تحلیل حاصل می‌شود.

به عنوان مثال، معادله موج را در نظر بگیرید

{displaystyle left(nabla ^{2}-{frac {1}{c^{2}}}{frac {partial ^{2}}{partial t^{2}}}right )u(mathbf {r} ,t)=0.}

جداسازی متغیرها با این فرض شروع می شود که تابع موج u ( r , t ) در واقع قابل تفکیک است:

{displaystyle u(mathbf {r} ,t)=A(mathbf {r} )T(t).}

با جایگزینی این شکل به معادله موج و سپس ساده سازی، معادله زیر را به دست می آوریم:

{displaystyle {frac {nabla ^{2}A}{A}}={frac {1}{c^{2}T}}{frac {mathrm {d} ^{2}T} {mathrm {d} t^{2}}}.}

توجه داشته باشید که عبارت سمت چپ فقط به r بستگی دارد ، در حالی که عبارت سمت راست فقط به t بستگی دارد . در نتیجه، این معادله در حالت کلی معتبر است اگر و تنها در صورتی که هر دو طرف معادله با یک مقدار ثابت برابر باشند. این استدلال در تکنیک حل معادلات دیفرانسیل جزئی خطی با جداسازی متغیرها کلیدی است. از این مشاهدات، دو معادله به دست می‌آید، یکی برای A ( r ) و دیگری برای T ( t ):

{displaystyle {frac {nabla ^{2}A}{A}}=-k^{2}}

{displaystyle {frac {1}{c^{2}T}}{frac {mathrm {d} ^{2}T}{mathrm {d} t^{2}}}=-k^ {2}،}

که در آن، بدون از دست دادن کلیت، عبارت - k 2 را برای مقدار ثابت انتخاب کرده ایم. (استفاده از هر ثابت k به عنوان ثابت جداسازی به همان اندازه معتبر است؛ - k 2 فقط برای راحتی در راه حل های حاصل انتخاب می شود.)

با تنظیم مجدد معادله اول، معادله هلمهولتز را به دست می آوریم:

{displaystyle nabla ^{2}A+k^{2}A=(nabla ^{2}+k^{2})A=0.}

به همین ترتیب، پس از جایگزینی ω = kc ، که در آن k عدد موج و ω فرکانس زاویه ای است (با فرض یک میدان تک رنگ)، معادله دوم تبدیل می شود.

{displaystyle {frac {mathrm {d} ^{2}T}{mathrm {d} t^{2}}}+omega ^{2}T=left({frac {mathrm { d} ^{2}}{mathrm {d} t^{2}}}+omega ^{2}right)T=0.}

اکنون معادله هلمهولتز برای متغیر فضایی r و یک معادله دیفرانسیل معمولی مرتبه دوم در زمان داریم. راه حل در زمان ترکیبی خطی از توابع سینوس و کسینوس خواهد بود که شکل دقیق آن توسط شرایط اولیه تعیین می شود، در حالی که شکل محلول در فضا به شرایط مرزی بستگی دارد . از طرف دیگر، تبدیل‌های انتگرال ، مانند تبدیل لاپلاس یا تبدیل فوریه ، اغلب برای تبدیل یک PDE هذلولی به شکلی از معادله هلمهولتز استفاده می‌شوند.

معادله هلمهولتز به دلیل ارتباط آن با معادله موج، در مسائلی در زمینه هایی از فیزیک مانند مطالعه تابش الکترومغناطیسی ، زلزله شناسی و آکوستیک به وجود می آید .

حل معادله هلمهولتز با استفاده از جداسازی متغیرها [ ویرایش ]

حل معادله فضایی هلمهولتز:

{displaystyle nabla ^{2}A=-k^{2}A} می توان برای هندسه های ساده با استفاده از جداسازی متغیرها به دست آورد .

غشای ارتعاشی [ ویرایش ]

آنالوگ دوبعدی رشته ارتعاشی غشای ارتعاشی است که لبه‌های آن بدون حرکت بسته شده است. معادله هلمهولتز برای بسیاری از اشکال اساسی در قرن 19 حل شد: غشای مستطیلی توسط سیمئون دنیس پواسون در سال 1829، مثلث متساوی الاضلاع توسط گابریل لامه در سال 1852، و غشای مدور توسط آلفرد کلبش در سال 1862. متییو ، منجر به معادله دیفرانسیل متییو .

اگر لبه‌های یک شکل پاره‌های خط مستقیم باشند، آن‌وقت یک راه‌حل به شکل بسته تنها در صورتی قابل بیان است که به صورت ترکیب خطی محدودی از امواج صفحه که شرایط مرزی را برآورده می‌کند (صفر در مرز، به عنوان مثال، غشاء گیره‌دار) قابل بیان باشد. ).

اگر دامنه دایره ای به شعاع a باشد ، مناسب است مختصات قطبی r و θ را معرفی کنیم . معادله هلمهولتز شکل می گیرد

{displaystyle A_{rr}+{frac {1}{r}}A_{r}+{frac {1}{r^{2}}}A_{theta theta }+k^{2} A=0.}

ممکن است شرط مرزی را تحمیل کنیم که A ناپدید می شود اگر r = a ; بدین ترتیب

{displaystyle A(a,theta )=0.}

روش جداسازی متغیرها منجر به حل آزمایشی شکل می شود

{displaystyle A(r,theta )=R(r)Theta (theta),}

که در آن Θ باید دوره ای 2 π باشد . این منجر به

{displaystyle Theta ''+n^{2}Theta =0,}

{displaystyle r^{2}R''+rR'+r^{2}k^{2}Rn^{2}R=0.}

از شرط تناوب نتیجه می شود که

{displaystyle Theta =alpha cos ntheta +beta sin ntheta,}

و n باید یک عدد صحیح باشد. جزء شعاعی R شکل دارد

{displaystyle R(r)=gamma J_{n}(rho)}

که در آن تابع بسل J n ( ρ ) معادله بسل را برآورده می کند

{displaystyle rho ^{2}J_{n}''+rho J_{n}'+(rho ^{2}-n^{2})J_{n}=0,}

و ρ = kr . تابع شعاعی J n برای هر مقدار n بی نهایت ریشه دارد که با ρm , n نشان داده می شود . شرط مرزی که A ناپدید می شود که در آن r = a برآورده می شود اگر اعداد موج مربوطه توسط

{displaystyle k_{m,n}={frac {1}{a}}rho _{m,n}.}

سپس راه‌حل کلی A شکل یک سری فوریه تعمیم یافته از عبارت‌ها را به خود می‌گیرد که شامل ضربهای Jn ( km , n r ) و سینوس (یا کسینوس) nθ است . این راه حل ها حالت های ارتعاش سر درام دایره ای هستند .

راه حل های سه بعدی [ ویرایش ]

در مختصات کروی، راه حل به صورت زیر است:

{displaystyle A(r,theta,varphi )=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }left(a_{ell m}j_{ell }(kr)+b_{ell m}y_{ell }(kr)right)Y_{ell }^{m}(theta،varphi).}

این راه حل از حل فضایی معادله موج و معادله انتشار ناشی می شود . در اینجا j ℓ ( kr ) و y ℓ ( kr ) توابع بسل کروی هستند و Y متر
ℓ( θ ، φ ) هارمونیک های کروی هستند (آبراموویتز و استگان، 1964). توجه داشته باشید که این فرم ها راه حل های کلی هستند و برای استفاده در هر مورد خاص نیاز به تعیین شرایط مرزی دارند. برای دامنه های بیرونی نامتناهی، ممکن است شرایط تشعشع نیز مورد نیاز باشد (سامرفیلد, 1949).

نوشتن r 0 = ( x , y , z ) تابع A ( r 0 ) مجانبی دارد

{displaystyle A(r_{0})={frac {e^{ikr_{0}}}{r_{0}}}fleft({frac {mathbf {r} _{0}}{ r_{0}}},k,u_{0}right)+oleft({frac {1}{r_{0}}}right){text{ as }}r_{0}to infty }

که در آن تابع f دامنه پراکندگی نامیده می شود و u 0 ( r 0 ) مقدار A در هر نقطه مرزی r 0 است .

راه حل های سه بعدی با توجه به عملکرد در یک صفحه دو بعدی [ ویرایش ]

با توجه به صفحه 2 بعدی که در آن A مشخص است، جواب معادله هلمهولتز به صورت زیر به دست می آید: [2]

{displaystyle A(x,y,z)=-{frac {1}{2pi }}iint _{-infty }^{+infty }A'(x',y'){ frac {e^{ikr}}{r}}{frac {z}{r}}left(ik-{frac {1}{r}}right),dx'dy',}

جایی که

  • {displaystyle A'(x',y')}راه حل در صفحه دو بعدی است،
  • ،{displaystyle r={sqrt {(xx')^{2}+(yy')^{2}+z^{2}}}،}

با نزدیک شدن z به صفر، تمام مشارکت های انتگرال به جز r=0 ناپدید می شوند. بدین ترتیب{displaystyle A(x,y,0)=A'(x,y)}تا یک ضریب عددی که با تبدیل مختصات انتگرال به قطبی می توان آن را 1 تأیید کرد..

این راه حل در تئوری پراش مهم است، به عنوان مثال در استخراج پراش فرنل .

تقریب پاراکسیال [ ویرایش ]

اطلاعات بیشتر: تقریب پاکت به آرامی تغییر می کند

در تقریب پاراکسیال معادله هلمهولتز، [3] دامنه مختلط A به صورت بیان می شود.

{displaystyle A(mathbf {r})=u(mathbf {r})e^{ikz}} که در آن u نشان‌دهنده دامنه با ارزش مختلط است که موج صفحه سینوسی نشان‌داده‌شده توسط ضریب نمایی را تعدیل می‌کند. سپس با یک فرض مناسب، شما تقریباً حل می کنید

{displaystyle nabla _{perp }^{2}u+2ik{frac {partial u}{partial z}}=0,} جایی که{textstyle nabla _{perp }^{2}{overset {text{ def }}{=}}{frac {partial ^{2}}{partial x^{2}}}+ {frac {partial ^{2}}{partial y^{2}}}}قسمت عرضی لاپلاس است .

این معادله کاربردهای مهمی در علم اپتیک دارد ، جایی که راه حل هایی ارائه می دهد که انتشار امواج الکترومغناطیسی (نور) را به صورت امواج سهمی یا پرتوهای گاوسی توصیف می کند . بیشتر لیزرها پرتوهایی را ساطع می کنند که این شکل را به خود می گیرند.

فرضی که بر اساس آن تقریب پاراکسیال معتبر است این است که مشتق z تابع دامنه u تابعی از z است که به آرامی متغیر است :

{displaystyle left|{frac {partial ^{2}u}{partial z^{2}}}right|ll left|k{frac {partial u}{partial z} }راست|.}

این شرط معادل این است که بگوییم زاویه θ بین بردار موج k و محور نوری z کوچک است: θ ≪ 1 .

شکل پاراکسیال معادله هلمهولتز با جایگزینی عبارت ذکر شده در بالا برای دامنه مختلط به شکل کلی معادله هلمهولتز به شرح زیر یافت می شود:

{displaystyle nabla ^{2}(uleft(x,y,zright)e^{ikz})+k^{2}uleft(x,y,zright)e^{ikz }=0.}

گسترش و لغو نتایج زیر را به همراه دارد:

{displaystyle left({frac {partial ^{2}}{partial x^{2}}}+{frac {partial ^{2}}{partial y^{2}}} راست)u(x,y,z)e^{ikz}+left({frac {partial ^{2}}{partial z^{2}}}u(x,y,z)right )e^{ikz}+2left({frac {partial }{partial z}}u(x,y,z)right)ik{e^{ikz}}=0.}

به دلیل نابرابری پاراکسیال ذکر شده در بالا، عبارت ∂ 2 u / ∂ z 2 در مقایسه با عبارت k · ∂ u / ∂ z نادیده گرفته شده است . این معادله پاراکسیال هلمهولتز را به دست می دهد. جایگزین کردن u ( r ) = A ( r ) e - ikz سپس معادله پاراکسیال برای دامنه مختلط اصلی A به دست می‌آید :

{displaystyle nabla _{perp }^{2}A+2ik{frac {partial A}{partial z}}+2k^{2}A=0.}

انتگرال پراش فرنل یک راه حل دقیق برای معادله پاراکسیال هلمهولتز است. [4]

معادله هلمهولتز ناهمگن [ ویرایش ]

دو منبع تابش در صفحه، که به صورت ریاضی با تابع f ، که در ناحیه آبی صفر است، داده می شود.

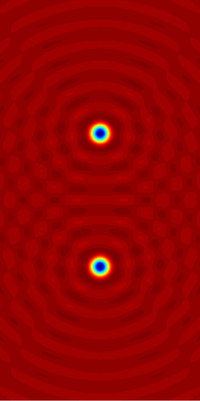
بخش واقعی میدان حاصل A , A حل معادله هلمهولتز ناهمگن است (∇ 2 + k 2 ) A = - f .

معادله هلمهولتز ناهمگن معادله است

{displaystyle nabla ^{2}A(mathbf {x} )+k^{2}A(mathbf {x} )=-f(mathbf {x} ) {text{ در }} mathbb {R} ^{n}،}

که در آن ƒ : R n → C تابعی با پشتیبانی فشرده و n = 1، 2، 3 است . این معادله بسیار شبیه به معادله پواسون غربال شده است ، و اگر علامت مثبت (در جلوی عبارت k ) باشد، یکسان خواهد بود. به علامت منفی تبدیل شدند.

برای حل این معادله به طور منحصربه‌فرد، باید یک شرط مرزی در بی‌نهایت مشخص شود، که معمولاً شرایط تابش سامرفلد است.

{displaystyle lim _{rto infty }r^{frac {n-1}{2}}left({frac {partial }{partial r}}-ikright)A( mathbf {x} )=0}

که درnابعاد فضایی، برای همه زوایا (یعنی هر مقدار از،{displaystyle theta,phi }). اینجا{displaystyle r={sqrt {sum _{i=1}^{n}x_{i}^{2}}}}جایی کهایکسمنx_{i}مختصات بردار هستندایکسmathbf {x}.

با این شرط، جواب معادله هلمهولتز ناهمگن است

{displaystyle A(mathbf {x} )=int _{mathbb {R} ^{n}}!G(mathbf {x} ,mathbf {x'} )f(mathbf {x' } ),mathrm {d} mathbf {x'} }

(توجه کنید که این انتگرال در واقع بیش از یک منطقه محدود است، زیرا f پشتیبانی فشرده دارد). در اینجا، G تابع گرین این معادله است ، یعنی حل معادله ناهمگن هلمهولتز با f برابر است با تابع دلتای دیراک ، بنابراین G برآورده می‌شود .

{displaystyle nabla ^{2}G(mathbf {x} ,mathbf {x'} )+k^{2}G(mathbf {x} ,mathbf {x'} )=-delta ( mathbf {x}،mathbf {x'} )in mathbb {R} ^{n}.}

عبارت تابع گرین به بعد n فضا بستگی دارد. یک نفر دارد

{displaystyle G(x,x')={frac {ie^{ik|xx'|}}{2k}}}

برای n = 1 ،

{displaystyle G(mathbf {x} ,mathbf {x'} )={frac {i}{4}}H_{0}^{(1)}(k|mathbf {x} -mathbf {x'} |)}

برای n = 2 ، که در آن H(1)
0تابع هانکل است و

{displaystyle G(mathbf {x},mathbf {x'} )={frac {e^{ik|mathbf {x} -mathbf {x'} |}}{4pi |mathbf {x} -mathbf {x'} |}}}

برای n = 3 . توجه داشته باشید که ما شرط مرزی را انتخاب کرده ایم که تابع سبز یک موج خروجی برای | است x | → ∞ .

در نهایت، برای n عمومی،

{displaystyle G(mathbf {x} ,mathbf {x'} )=c_{d}k^{p}{frac {H_{p}^{(1)}(k|mathbf {x} -mathbf {x'} |)}{|mathbf {x} -mathbf {x'} |^{p}}}}

جایی که {displaystyle p={frac {n-2}{2}}}و{displaystyle c_{d}={frac {1}{2i(2pi )^{p}}}}. [5]

همچنین ببینید [ ویرایش ]

  • معادله لاپلاس (مورد خاصی از معادله هلمهولتز)
  • گسترش ویل

یادداشت ها [ ویرایش ]

  1. ↑ معادله هلمهولتز ، از دایره المعارف ریاضیات .
  2. ↑ مهرابخانی، س.، و اشنایدر، تی (1396). آیا پراش Rayleigh-سامرفیلد همیشه مرجع دقیقی برای الگوریتم های پراش پر سرعت است؟ Optics express, 25(24), 30229-30240.
  3. ^ جی دبلیو گودمن. مقدمه ای بر اپتیک فوریه (ویرایش دوم). صص 61-62.
  4. ^ گرلا، آر (1982). "انتشار فرنل و پراش و معادله موج پاراکسیال". مجله اپتیک . 13 (6): 367-374. Bibcode : 1982JOpt...13..367G . doi : 10.1088/0150-536X/13/6/006 .
  5. ↑ بیورن انگکویست؛ هونگکای ژائو (نوامبر 2018). "تفکیک پذیری تقریبی تابع گرین از معادله هلمهولتز در حد فرکانس بالا". ارتباطات در ریاضیات محض و کاربردی . 71 (11): 2220-2274. doi : 10.1002/cpa.21755 .

منابع [ ویرایش ]

  • آبراموویتز، میلتون؛ Stegun، Irene، ویرایش. (1964). کتاب راهنمای توابع ریاضی با فرمول ها، نمودارها و جداول ریاضی . نیویورک: انتشارات دوور. شابک 978-0-486-61272-0.
  • رایلی، KF; هابسون، نماینده مجلس؛ بنس، اس جی (2002). "فصل 19". روشهای ریاضی فیزیک و مهندسی نیویورک: انتشارات دانشگاه کمبریج. شابک 978-0-521-89067-0.
  • رایلی، کی اف (2002). "فصل 16". روش های ریاضی برای دانشمندان و مهندسان . ساوسالیتو، کالیفرنیا: کتاب های علوم دانشگاهی. شابک 978-1-891389-24-5.
  • صالح، بها EA; تیچ، مالوین کارل (1991). "فصل 3". مبانی فوتونیک . سری وایلی در اپتیک خالص و کاربردی. نیویورک: جان وایلی و پسران. صص 80-107. شابک 978-0-471-83965-1.
  • سامرفلد، آرنولد (1949). "فصل 16". معادلات دیفرانسیل جزئی در فیزیک . نیویورک: انتشارات آکادمیک. شابک 978-0126546569.
  • هاو، ام اس (1998). آکوستیک فعل و انفعالات سیال-ساختار . نیویورک: انتشارات دانشگاه کمبریج. شابک 978-0-521-63320-8.

پیوندهای خارجی [ ویرایش ]

  • معادله هلمهولتز در EqWorld: دنیای معادلات ریاضی.
  • "معادله هلمهولتز" ، دایره المعارف ریاضیات ، انتشارات EMS ، 2001 [1994]
  • غشای دایره‌ای ارتعاشی اثر سم بلیک، پروژه تظاهرات ولفرام .
  • توابع گرین برای موج، معادلات هلمهولتز و پواسون در یک حوزه بی کران دو بعدی

https://en.wikipedia.org/wiki/Helmholtz_equation

ریاضیات...
ما را در سایت ریاضیات دنبال می کنید

برچسب : نویسنده : 9math1342d بازدید : 178 تاريخ : چهارشنبه 27 دی 1402 ساعت: 20:15

آرشیو مطالب

پيوندهای روزانه

لینک دوستان

خبرنامه